Solving 3D Path Planning problem using Adapted-RRT and GWO for UAVs
3D path planning problem for UAVs has been among very hot topics for both data scientists and robotics engineers for last several decades.
Main purpose of algorithms that try to solve this problem is to find collision free and optimal trajectory for UAVs. Taxonomy of well known algorithms that has been proposed over the years has been shown below,
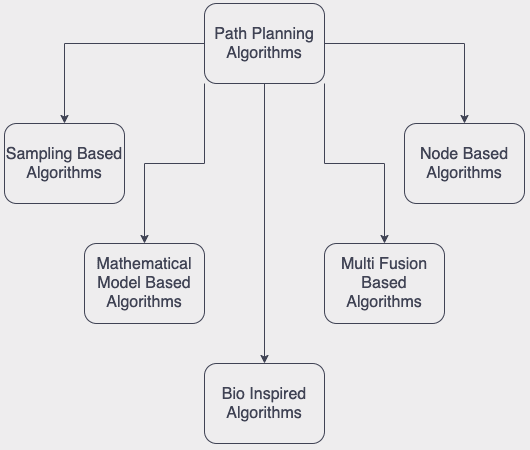
Due to taxonomy, proposed algorithm is suitable to Bio Inspired Algorithms category that mimics swarms of grey wolves.
Proposed Method(GWO and RRT like algorithm)
Details of GWO(Gray Wolf Optimizer) was explained in my previous blog. You can find more information about GWO and source code in Java in this blog Imagine population(alpha, beta, delta and omega wolves) each individuals of UAVs, dimension as trajectory in our case. Each element of Optimization Matrix is distance between next and current points of wolf. Algorithm is suitable for 2D Path Planning problems as well. All we need to do is assign one axis of cordinates of wolves to 0 while initialization. GWO algorithm lets us to define coordinates of next pace of UAVs. But it shouldn't be forgotten that Optimization Algorithms are designed to minimize/maximize fitness values using fitness functions(Sphere function etc). In this problem we used fitness function below,
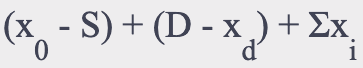
i - from 0 to d(dimension of Optimization Matrix), S and D are relevantly coordinates of Source and Destination points.
To calculate distance between points euclidean metrics is used but other metrics systems also can be implemented to find distances. Surely, path planning problem can be solved using only GWO but we would encounter trouble that GWO tries to combine all the points in one point to find minimum trajectory lenght. Let's say dimension of Optimization Matrix is equal to 10 so result would be like,
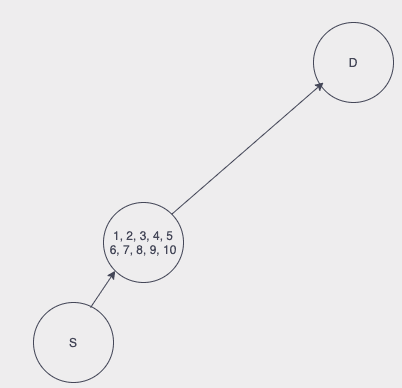
So numbers from 1 to 10 indicate the steps of UAVs from source to destination. But all the steps are located in the same coordinates by GWO.
This is the phase where RRT(Rapidly Exploring Random Tree) like algorithm comes and joins to the game. It is achieved to prevent that UAVs to stay at the same coordinates along dimension by controlling each steps. If current step point has been visited by UAV before we change current point in the direction of Destination by
Formula above lets to move to destination by the same lenght of phases each time. But in order to accomplish minimum trajectory lenght we multiply r with (a + b).
a - number from GWO goes down from 2.0 to 0.0 over the iterations, at the end of iterations a is almost equal to 0. It means r is also equal to 0. To get ahead of this we add number b that is equals to 0.5 with number a. So r would never be 0.0.
Result
Demonstration example for algorithm in 5 dimensions be like,
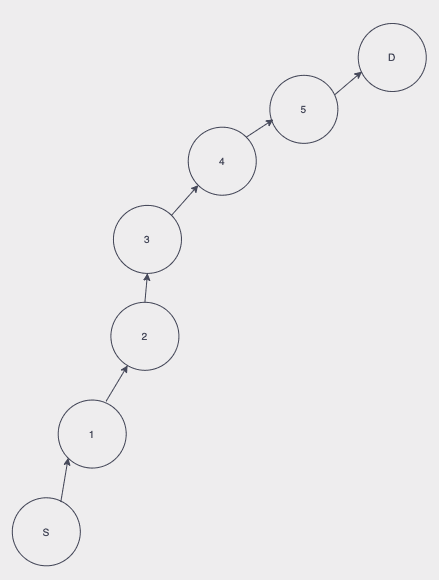
For Benchmark results at the end of iterations we find positions of alpha wolf(coordinates that UAV pass through). Results after 500 iteration for S(0.0, 0.0, 0.0) and D(100.0, 100.0, 100.0) should be like for 30 population and 10 dimensions:
Initialization, alpha's fitness value: 1755.012467011726
Initialization, alpha values:
[[43.600411765322775, 7.661902485546923, 38.86637559165679], [64.68534567376066, 18.22820299491844, 42.095895892189716], [29.735038835090634, 33.35684142153366, 69.60048205710501], [50.57620273039834, 56.75672526657907, 18.14024001257779], [83.92291978435703, 36.122856677739456, 55.83461628039294], [37.30995020225119, 95.62449566549978, 26.836141309770035], [47.6472985651047, 54.93388338455847, 9.088804428061925], [58.58268956314632, 14.837810722094192, 58.42348885984282], [88.24129933375971, 93.73590209740374, 63.979081720299114], [65.19382809451533, 24.42031416077255, 66.2081160155354], [55.05809141201077, 66.68872048958482, 82.1198854683015], [54.82835625910163, 71.94370439944015, 93.9048431102944], [39.477553496763505, 52.06092208101929, 76.15079454301767], [67.55262167820257, 85.79043755958999, 13.126433263181381], [33.18596598820053, 78.12062511516675, 11.878112021810905], [41.77839992558695, 25.85775960795904, 26.36409324541925], [30.770868814353804, 93.30476963965913, 72.15698837469444], [43.117145184016294, 95.98720101925484, 52.76532657716876], [46.66040481954082, 98.83210913541795, 42.57444559375544], [77.04219807208564, 63.883629016924694, 7.878287265167716], [62.121681456104064, 72.97214918236995, 19.60688524676135], [30.386484413241778, 37.114156170010304, 20.645757497663364], [1.9197735485338763, 75.30437243735061, 2.2836596741605653], [40.89995109646218, 77.5789374628285, 12.331833425092364], [71.01942310160013, 49.09679797544032, 31.2451543723829], [7.534213947772528, 63.439245547284095, 33.47286737506746], [85.26405510517719, 7.6853744906355885, 99.38080111312361], [45.65984982233775, 55.877279479131715, 11.771332018526214], [74.3580816494911, 93.4185560236204, 8.098602867826354], [84.58918869411967, 19.438263995336246, 81.19483897244622]]
After 500 iterations, alpha's fitness value: 216.71831188136198
After 500 iterations, alpha's values:
[[35.090490943159544, 45.52237831617591, 29.71771683546812], [37.24745867816017, 47.33269045624587, 29.71771683546812], [39.4044264131608, 49.14300259631583, 29.71771683546812], [41.561394148161426, 50.95331473638579, 29.71771683546812], [43.71836188316205, 52.76362687645575, 29.71771683546812], [45.87532961816268, 54.57393901652571, 29.71771683546812], [48.03229735316331, 56.384251156595674, 29.71771683546812], [50.189265088163936, 58.194563296665635, 29.71771683546812], [52.34623282316456, 60.004875436735595, 29.71771683546812], [54.50320055816519, 61.815187576805556, 29.71771683546812], [56.66016829316582, 63.62549971687552, 29.71771683546812], [58.817136028166445, 65.43581185694548, 29.71771683546812], [60.97410376316707, 67.24612399701543, 29.71771683546812], [63.1310714981677, 69.05643613708538, 29.71771683546812], [65.28803923316833, 70.86674827715534, 29.71771683546812], [67.44500696816897, 72.67706041722529, 29.71771683546812], [69.6019747031696, 74.48737255729525, 29.71771683546812], [71.75894243817024, 76.2976846973652, 29.71771683546812], [73.91591017317087, 78.10799683743515, 29.71771683546812], [76.0728779081715, 79.9183089775051, 29.71771683546812], [78.22984564317214, 81.72862111757506, 29.71771683546812], [80.38681337817277, 83.53893325764501, 29.71771683546812], [82.5437811131734, 85.34924539771498, 29.71771683546812], [84.70074884817403, 87.15955753778493, 29.71771683546812], [86.85771658317465, 88.9698696778549, 29.71771683546812], [89.01468431817528, 90.78018181792486, 29.71771683546812], [91.1716520531759, 92.59049395799482, 29.71771683546812], [93.32861978817654, 94.40080609806478, 29.71771683546812], [95.48558752317716, 96.21111823813474, 29.71771683546812], [97.6425552581778, 98.0214303782047, 29.71771683546812]]
Negotiation
Alternative algorithm with static stations to solve this problem is coming soon
Appendices
• Source codePlease rotate your device!